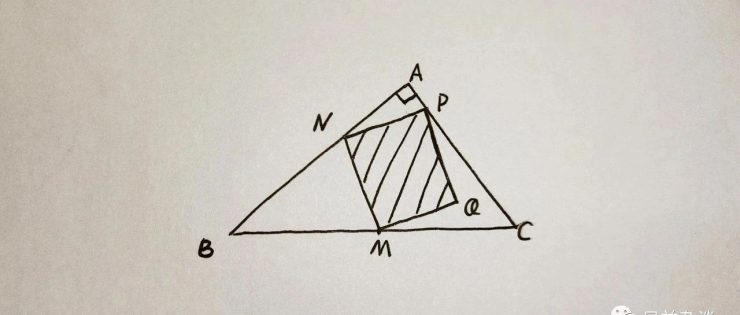
如图，三角形ABC是直角三角形，M是斜边BC的中点，MNPQ是正方形，N在AB上，P在AC上，如果AB的长度是12，AC的长度是8，那么正方形MNPQ的面积是多少？

上面这题是今年某附中小升初考试第12题，是个微不足道的填空题，大眼一瞅，条件中有直角三角形、斜边中点、正方形，要素过多，分明像是有手就能做的题型。

可惜日益君多少不是太行，类似这种问题，积习难改，第一反应就是基于解析手法强行计算，毕竟硕大的直角在那摆着，不用白不用。果断基于直角顶点建立平面直角坐标系，所需的点坐标几乎都是现成的，一通常规操作，波澜不惊，无比丝滑，直到此刻，日益君还没有意识到题目的严重性……‍‍‍‍

下一刻，面色瞬间凝重，好家伙，二元二次方程组？消元之后，惊现一元四次方程，乖乖不得了，过于凶残……‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

幸好试卷上的题图画得比较标准，定睛一看，N似乎是AB的三等分点，哆哆嗦嗦把a=4代入方程检验，居然给蒙对了，意外不？惊喜不？猜到结果之后，装模作样因式分解把解答过程强行续上……‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

但是吧，此处的瞪眼法毫无科学性可言，跟极端假设之类的合理猜测完全不挨着，作为一个受过正经九年义务教育的人，不该这么乱来