小学奥数五大几何模型汇总,学会他,轻快搞定考试!

HAPPY
NEW
YEAR
几何作为数学学习中不可或缺的内容,贯穿于小学、初中、高中乃至大学的数学中,而在小学阶段,平面几何又是小初考试必考内容,往往以大题的形式出现,在近几年小初考试中所占比例达到30%-40%,而且涉及到的知识难度也有逐年增大的趋势。
虽然几何题形式多样,但通过总结归纳,掌握基本的几何模型,便能有助于办理更多新题、难题,这里,我们便一起探究小初常考模型:
等 积 模型
一、等积模型
①等底等高的两个三角形面积相当;
②两个三角形高相等,面积比即是它们的底之比;
两个三角形底相等,面积比即是它们的高之比;
如右图
③夹在一组平行线之间的等积变形,如下图;
反之,如果,
则可知直线ab平行cd于.
④等底等高的两个平行四边形面积相等(长方形和正方形不妨看作特殊的平行四边形);
⑤三角形面积等于与它等底等高的平行四边形面积的一半;
⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之
典型例题:
例1:如图,正方形ABCD与正方形CEFG相连,正方形ABCD的边长为8厘米,求三角形ADG的面积?
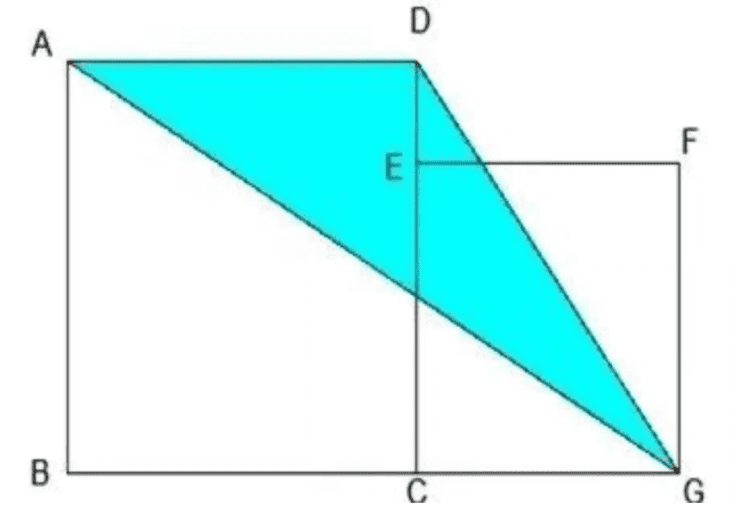
点拨:连接AC做辅助线。
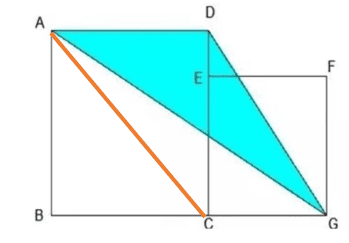
解析:
S△ADG与S△ADC的同底同高,则S△ADG与S△ADC的面积相等;
故S△ADG=S△ADC=8×8÷2=32平方厘米。
蝶形定理
二、蝶形定理
1. 任意四边形中的比例关系(“蝶形定理”):
S1:S2=S4:S3或S1×S3=S2×S4
AO:OC=S1:S4=S2:S3=(S1+S2):(S4+S3)
蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.
2. 梯形中比例关系(“梯形蝶形定理”):
①S1:S2=a2:b2
②S1:S3:S2:S4=a2:b2:ab
③s的对应份数为(a+b)2
典型例题:
例2:求下图阴影部分面积:
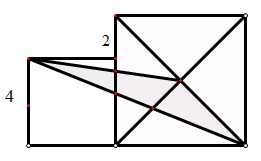
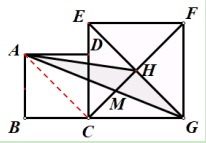
点 拨:如何将阴影部分面积转化为我们熟悉并且容易求的图形面积,就需要我们构造蝴蝶模型。
解 析:连接AC,AC与EG都为正方形对角线
所以:AC∥HG
故四边形ACGH为梯形(梯形是指只有一组对边平行的四边形)
△AMH和△CMG是梯形中的两翼,梯形蝴蝶模型中,两翼面积相等
因此,S△AMH=S△CMG
阴影部分面积转化为S△CHG=¼S正方形=¼×6×6=9
燕 尾 模 型
从三角形一个顶点向对边上任意一点上画线段,在线段上任取一点组成的图形面积也会有如下关系:
S△ABO:S△ACO
=S△OBD:S△OCD
=S△ABD:S△ACD
=BD:CD
题目经常会出现隐藏的燕尾模型,需要我们去构造燕尾,并且可能会有两个燕尾综合考察。
典型例题:
例3:S△ABC=12,D点为三等分点,E点为平分点,BD=1,DC=2,AE=1,求阴影部分面积:
点 拨:在三角形中,如果用不了公式、割补等办法求面积,可尝试用模型求解。如果边上分点与顶点连线考虑燕尾模型。一般用标份数方法。
解 析:连接FC
已知BD:DC=1:2 (两外比)→S△BDF:S△CDF=1:2
设S△BDF为1份,S△CDF为2份
AE:EC=1:1 → S△ABF:S△CBF=1:1
又因为S△BFC为3份,所以S△ABF为3份
BD:DC=1:2 → S△ABF:S△AFC=1:2
因为S△ABF为3份,所以S△AFC为6份
AE:EC=1:1 → S△AEF:S△ECF=1:1=3份:3份
由图将三角形分为3+3+3+1+2=12份
12÷12×4=4 阴影部分面积是4份
鸟 头 模 型
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形常见图形有:
有
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
例5:如图,已知三角形ABC面积为1,延长AB至D,使BD=AB,延长BC至E,使CE=2BC,延长CA至F,使AF=3AC,求三角形DEF的面积。
点 拨:已知三角形ABC与其他未知的三个三角形都分别组成了鸟头模型,并且知道线段的比例关系,可用鸟头模型解题。
解 析:
相似模型
(一)金字塔模型
①;
②:
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:
⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;
⑵相似三角形的面积比等于它们相似比的平方;
⑶连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.
相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.
在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.
典型例题:
例4
如图是由边长分别为5厘米和4厘米的两个正方形拼成,图中阴影部分的面积是多少平方厘米?
点 拨:解:因为图形是由两个正方形拼成的,所以AH∥CD,所以可得三角形AHG与三角形CDG相似,相似比是AH:CD=5:4,
解 析:
据此可得HG:GC=5:4,所以HG:HC=5:9,
所以HG=5/9×5=9/25(厘米),
则:GF=9/25﹣(5﹣4)=16/9(厘米),
所以阴影部分的面积是:9/16×4÷2=9/32(平方厘米),
本文链接: https://www.yizhekk.com/0130237968.html








