在通过对尖子生的培养，使他们在原来的水平上有一个大的提高，熟练掌握一点儿知识技能，使之在数学领域有创新有发展，将来为社会做出自己特殊的贡献。

每期三道有代表性的题目，奉献给六年级同学，期望对你参加“拔尖生”选拔有所帮助。 

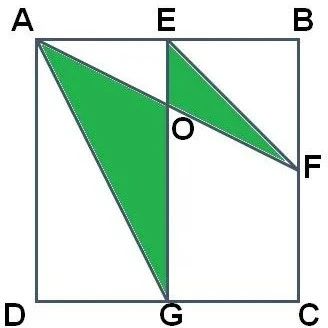
232. 已知e、f、g为正方形abcd边上的中点，ΔAOG比Δefo的面积大16平方厘米，求正方形abcd面积。

233. 如图，直角三角形abc的三条边分别为9cm、12cm、15cm，将其直角边ac半数到斜边ab上，使ac与ac’重合，未重叠部分的面积是多少平方厘米？

参考答案难题详解

232.解题思路

ΔAGE与ΔAFE同底AE，前者的高为正方形边长，后者的高为正方形边长的1/2。因此，ΔAFE是ΔAGE面积的1/2。

   ΔAEO为ΔAGE与ΔAFE的共有部分，所以， ΔAGE与ΔAFE的面积差也是ΔAGO与ΔEFO的面积差，即16平方厘米。

   看图知，ΔAGE为正方形面积的1/4，则ΔAFE为正方形面积的1/8。

   这两个分率都以正方形面积为单位“1”，抓住二者的数量差与对应的分率差，即可求出单位“1”——正方形面积：

16÷（1/4-1/8）=128平方厘米

233.解题思路

此题应抓住图中3个三角形面积比的关系解答为宜。

 直角边AC对折到斜边AB上，如下图：

  这将直角三角形ABC分成三部分：

∆ACD、∆ADC’、∆DBC’。

其中∆ACD=∆ADC‘（重叠部分），

∆ADC’与∆DBC’为等高模型（共边模型），它们底边的比就是二者面积比：

9：（15-9）=3：2

  因而，∆ACD、∆ADC’、∆DBC’三者的面积比为：

  3：3：2

  如下图：

 直角三角形ABC的面积是：

   12×9÷2=54平方厘米

  则未重叠部分∆DBC’的面积为：

   54×2/(3+3+2)=13.5平方厘米

234.解题思路

ΔABP+ΔCDP为平行四边ABCD面积的一半；