火柴棒游戏

小刚用火柴搭了一个错误的算式：1+1+十一=1，请你移动一根火柴使算式成立。

下图是由小正方体搭拼的图形，请你数一数一共用了几许个小正方体？（有条件的可以摆一摆，数一数）

妈妈买了一个书包和一个文具盒，她付给售货员50元，售货员找回5元。已知书包的代价是文具盒的4倍，请问：书包和文具盒各多少钱？

一年级

【答案】见解析。

【解析】

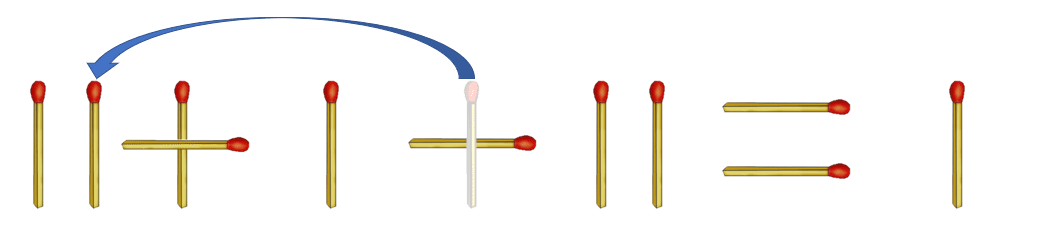
方法1：将从左往右数第二个加号中竖着的火柴移动到第一个加数1的旁边，算式变成11+1-11=1。如下图所示：

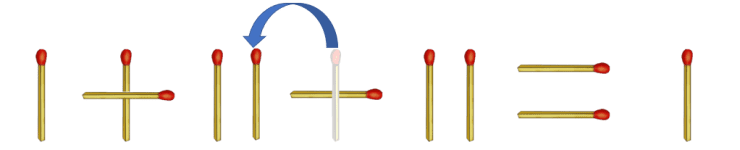
方法2：将从左往右数第二个加号中竖着的火柴移动到第二个加数1的旁边，算式变成1+11-11=1。如下图所示：

二年级

【答案】30个。

【解析】通过题目要求和立体图形可知：小正方体一共分四层，先把每一层小正方体的个数数出来，然后加起来就是总数量；从最下面的一层开始，第一层4×4=16（个）；第二层3×3=9（个）；第三层2×2=4（个）；最上面一层是1个；16+9+4+1=30（个）。

三年级

【答案】 书包36元，文具盒9元。

【解析】由“妈妈付给售货员50元，售货员找回5元”可以推出，书包和文具盒的总钱数是50-5=45（元）；又因为“书包的价格是文具盒的4倍”，可以把文具盒的价格看作1份，那么书包的价格是这样的4份，书包和文具盒的总钱数相当于4+1=5份，如图：

     文具盒的价格是其中1份的钱数，即45÷（4+1）=9（元）；书包的价格是文具盒的4倍，即9×4=36（元）；也可以用总钱数减去文具盒的钱数，即45-9=36（元）。

四年级

【答案】A、B两地相距228千米。

【解析】根据题意“甲每小时行54千米,乙每小时行45千米”可知：甲比乙每小时多行54-45=9（千米）；又根据“当甲距B地还有12千米时,乙距B地还有48千米”可知：这时甲比乙多行了48-12=36（千米）。由此可知，此时两人行驶的时间是36÷9=4(小时)。所以A、B两地相距54×4+12=228(千米)或45×4+48=228(千米)。

五年级

【答案】汽车13时到达乙地的。

【解析】根据题意，画线段图。

      观察上图，货车从A点到B点的时间，正好是汽车从甲地到乙地的时间，在相同的时间内，两车的路程差为：45×2+30=120（km）。两车的速度差为：75-45=30（km/h），根据“追及时间=路程差÷速度差”，可得追及时间是：120÷30=4（小时），即汽车从甲地到乙地的时间为4小时。已知汽车是9时出发，因此，汽车在13时到达乙地的。

六年级

【答案】6秒。

【解析】为便于研究我们把正方形命名为正方形ABCD,如下图所示。开始时甲落后乙：10×2=20（米）；那么当甲落后乙10米时，甲追了20-10=10（米）。甲比乙每秒钟多走5-3=2（米），那么此时两人所用的时间为：10÷2=5（秒）；即：甲走了5×5=25（米），此时甲位于CD的中点处，而乙走了3×5=15（米），乙位于AD中点处。

    因为甲比乙快，所以当甲走到D时，乙仍在AD上，这时甲第一次看见乙。那么甲从CD的中点处再用1秒钟走5米就能第一次看见乙。因此，经过5+1=6（秒），甲才能第一次看见乙。